Hyperparameters Definition
The hyperparameters of a model are the values of the settings used during the training process. They are generally not obtained from the data, so they are usually indicated by the data scientist. The optimal value of a hyperparameter cannot be known a priori for a given problem.
So you have to use generic values, generic rules, the values that have worked previously in similar problems, or find the best option through trial and error. Cross-validation is a good option to look for hyperparameters.
Examples of Hyperparameters
When training a machine learning model, the values of the hyperparameters fix so that the parameters obtain with them. Some examples of hyperparameters used to train models are:
- The learning degree in the gradient descent algorithm.
- The number of neighbours in k-nearest neighbours (k-nn).
- The maximum depth in a decision tree.
Optimization of Hyperparameters
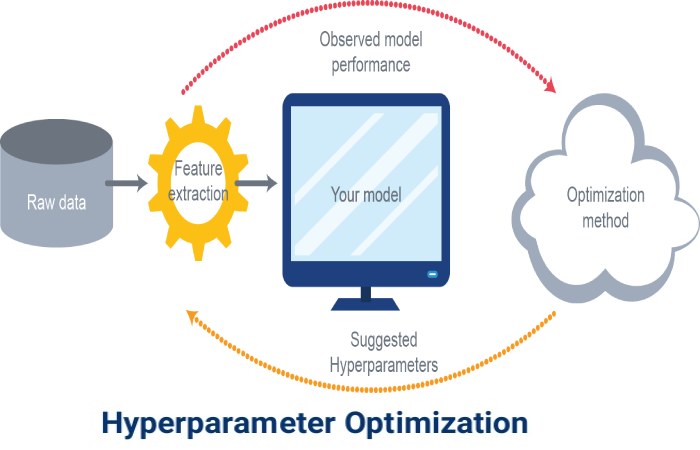
Hyperparameters can have a direct influence on the training of machine learning algorithms. Therefore, to get maximum performance, it is important to understand how to optimize it. Here are some common plans for optimizing hyperparameters:
Grid Finder: Look for a set of manually preset hyperparameters to get the best performing hyperparameter. Use this value. (This is the traditional method)
Random search: Similar to grid search, but replaces the exhaustive search with a random search. This can overcome grid search when only a small number of hyperparameters are needed to optimize the algorithm.
Bayesian Optimization: Creates a probabilistic model of the mapping of the function from the values of the hyperparameters to the objective evaluated in a validation set.
Gradient-Based Optimization: Calculate the gradient using hyperparameters, then optimize the hyperparameters through gradient ancestry.
Evolutionary optimization: Uses evolutionary algorithms (e.g., genetic functions) to find the space of possible hyperparameters.
What is the Tuning of Hyperparameters?
Hyperparameters: Vanilla linear regression does not have hyperparameters. Linear regression variants (crest and loop) have regularization as a hyperparameter. The decision tree has a maximum depth and a minimum number of observations on the sheet as hyperparameters.
Optimal Hyperparameters: Hyperparameters control overfitting and misfitting the model. Optimal hyperparameters often differ for different data sets. To obtain the best hyperparameters, the following steps are followed:
1. For each proposed hyperparameter configuration, the model evaluated.
2. The hyperparameters that give the best model selection.
Hyperparameter Search: Grid Search selects a grid of hyperparameter values and evaluates all of them. Assumptions require specifying the minimum and maximum values for each hyperparameter. Random search randomly evaluates a random sample of points on the grid.
It is more efficient than the grid search. Smart hyperparameter tuning selects some hyperparameter parameters, evaluates the validation matrices, tunes, and re-evaluates the validation matrices. Examples of smart hyperparameters are Spearmint (optimising using Gaussian processes) and Hyperopt (it optimising using tree-based estimators).
Types of Hyperparameters
When you choose to work with a specific ML algorithm, you must adapt its configuration by defining the hyperparameters. Some of them relate to the architecture or the specification, to the definition of the model itself. For example, the number of sheets for neural networks, the nucleus selection for Gaussian processes or the number of K neighbours in K-Nearest Neighbors.
This type of hyperparameter determines the shape of the model train, i. p. for example, the shape of the tuple of parameters to optimize. In addition, others will control the learning process—for example, the learning rate for various cases such as pulse algorithms.
Once all it is ready, the learning step can take place. And, as a result, the model parameters obtain, which will be applied to produce predictions when new features need to address. These parameter tuples will be the centroid of the clusters for K-Means, the split and end nodes for any tree algorithm, or the support vector coefficients for support vector machines. It will not be present in the prediction step.
It required to vary considerably depending on the ML algorithm. Some of them don’t even require it, as is the case with linear regression. Some can define by definition without question. The distance metric used in PCA, for instance, usually derive directly from our problem.
Although any hyperparameter can affect the final model, only a few of them are more likely to affect it aggressively. Some people favour calling only those related to training.
On the other hand, other experts do not consider hyperparameters as those that attach directly or easily, but only those that will optimize—open debate. I use the hyperparameter to refer to every element you need to configure outside the ML algorithm, as they are all potentially subject to optimization.
Difference between Parameters and Hyperparameters

Let’s comprehend the difference between parameter and hyperparameter with an example. When learning, for example, to drive, you must conduct learning sessions with an instructor who will teach you.
Here they train you with the help of the instructor. The instructor accompanies you throughout the lessons. They help him practice driving until he feels safe enough and can drive on the road on his own.
Once trained and able to drive, you will not need to train by the instructor. In this scenario, the instructor is the hyperparameter, and the student is the parameter.
As seen previously, the parameters are the variables whose value the system estimates during training. The hyperparameter values predefine. The hyperparameter values are independent of the data set. These values do not change during training.
The hyperparameter not part of the train or final model. The model parameter values estimated during training save with the trained model. The hyperparameter values use during training to estimate the value of the model parameters.
It is an external configuration variable, while model parameters are internal to the system. Since the hyperparameter values not save, the trained or final models not used for prediction. However, the model parameters use when making predictions.
Conclusion
A hyperparameter is a configuration variable external to the model. It is set manually before training the model with the historical data set. Its value cannot evaluate from the datasets.
It is not possible to distinguish the best value of the hyperparameter. But we can use general rules or select a worth with trial and error for our system.
It touches on the speed and correctness of the model training process. Different systems need different numbers of it. Simple systems may not need it.
Also Read: What is Telegraph? – History, Invented, Work, and More


